What is the Fundamental Data Structures: Arrays?

Today, technology is improving and changing in a blink of an eye, and things become irrelevant and obsolete in a matter of days.

In the era of different cloud providers, frameworks, libraries and prebuilt assets, programming beginners might ask themselves whether it’s worth investing their time into learning Data Structures?

I’ve heard some people claim that you do not need to know what a linked list, a heap or a B+ tree is, in order to be a programmer. This is true, in a way

However, not so while ago, my great curiosity led me to the GitHub repository of React.js library to see what the famous VDOM and diffing implementation looks like.

I was disappointed. While I managed to understand the concept of certain things, most of the implementation was not clear to me. It looked like the creators of React.js had a genius for algorithms and data structures, especially for trees.

That’s when I realised why some of the largest tech companies such as Facebook, Microsoft, Amazon, Google, and others insist on excellent knowledge of data structures and algorithms.

Facebook creators would not have created React.js as good as it is today if there hadn’t been for their data structures and algorithms knowledge. Why did I highlight as good as it is today?

Because, yes, they would’ve managed to create it, but it probably wouldn’t have been as efficient and popular as it is today. And the same stands for SQL Server creators, Google Search Engine creators, gentlemen Larry Page and Sergey Brin, and so on.

These and some other thoughts made me break the chains of modern software development and go back to the core of software engineering.

I set off on a journey of exploring the heart of some of the best software products, as well as existing data structures in different programming languages, whose API-s we are clients of, which is mostly taken for granted.

In addition, I also wanted to share the things I am about to learn on this journey with others.

We simply have to start from the arrays.

Arrays are one of the fundamental, simplest, perhaps most used data structures and a very important concept in programming.

But, what is the definition of a data structure in the first place?

A data structure is nothing more than a way of organising data in our computer’s memory.
We can organise different data in different ways depending on the nature of the problem that we are trying to solve.
And it turns out that how we organise the data can be a critical factor in its efficient handling, and transitively, our software performance.

But before we start talking about arrays and their advantages and disadvantages in detail, let’s remind ourselves of how computer memory works in order to understand arrays better.

Computer Memory Basics - RAM (Random Access Memory)

When a program is executing it has to store variables somewhere, regardless of whether they are numbers, strings, or any other type of data.

Variables are stored in the computer's main memory - RAM (Random Access Memory), and further in the text we’re mostly going to refer to it just as memory.

The memory is divided into slots where each slot can store 1 byte of data. Each slot is associated with a number that represents its location in memory - its memory address.

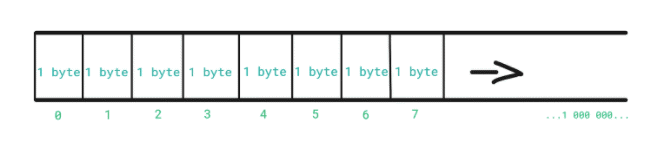
On the other hand, we have a CPU which is connected to a component called Memory Controller.

Memory Controller is the component that performs reading from and writing into the memory.
Besides the fact that this component works hard to help us make sure that we do not lose any data from the memory during a program execution, it actually has a direct connection with each and every memory slot.

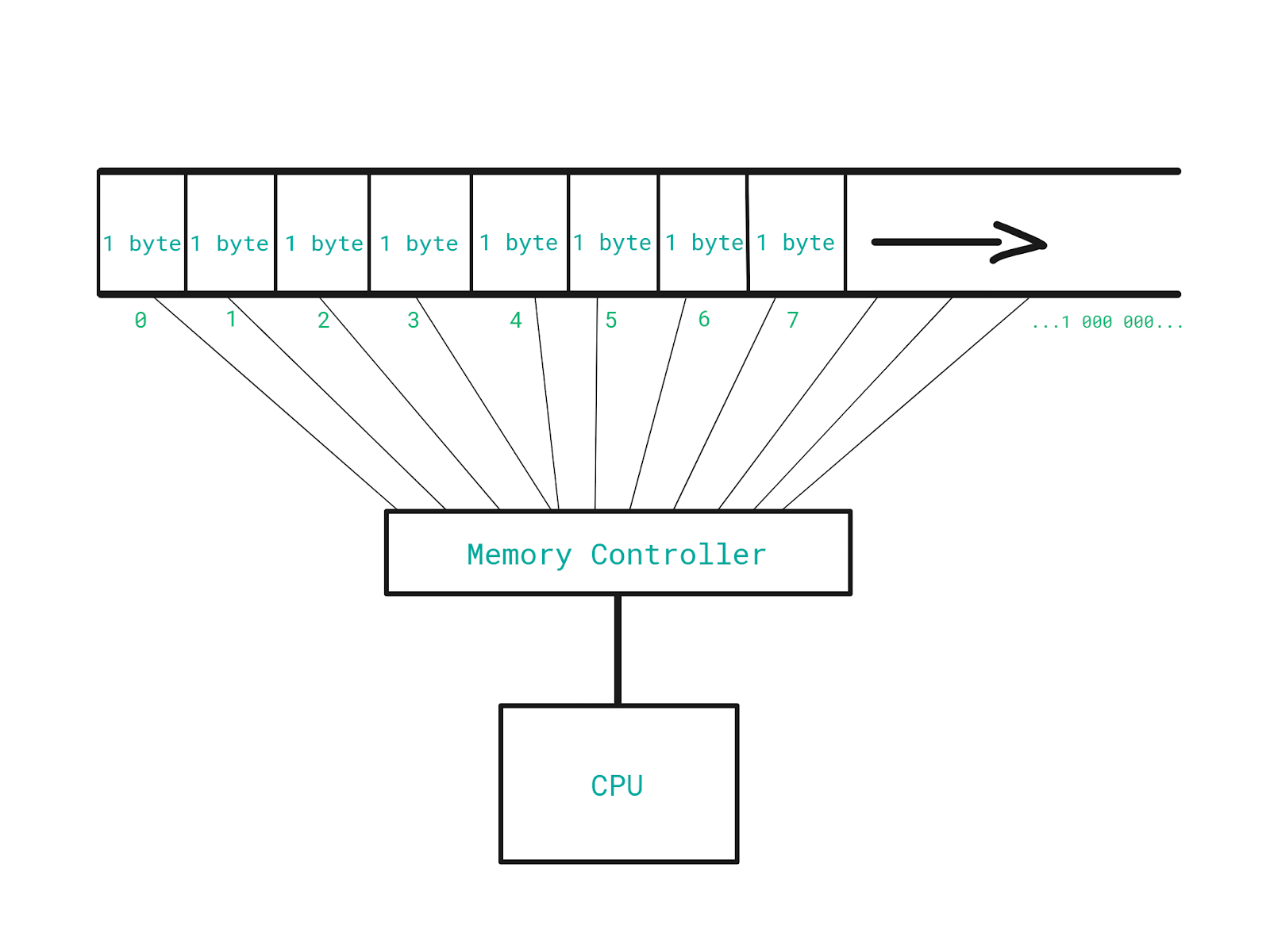
What does that mean?

If we have a direct connection to each and every memory slot (address), we can access the address 201 and then the address 99 998 instantly, without having to go step by step, one address at a time, in order to get to the targeted one.

Even though the memory controller can jump back and forth between different addresses very efficiently, programs tend to access memory addresses that are closer to each other.
Computers are optimised to get a boost in speed when they’re accessing adjacent memory addresses.

How?

The CPU has this tiny but super-fast memory called cache. This is where the CPU stores the data it has recently read from the memory.

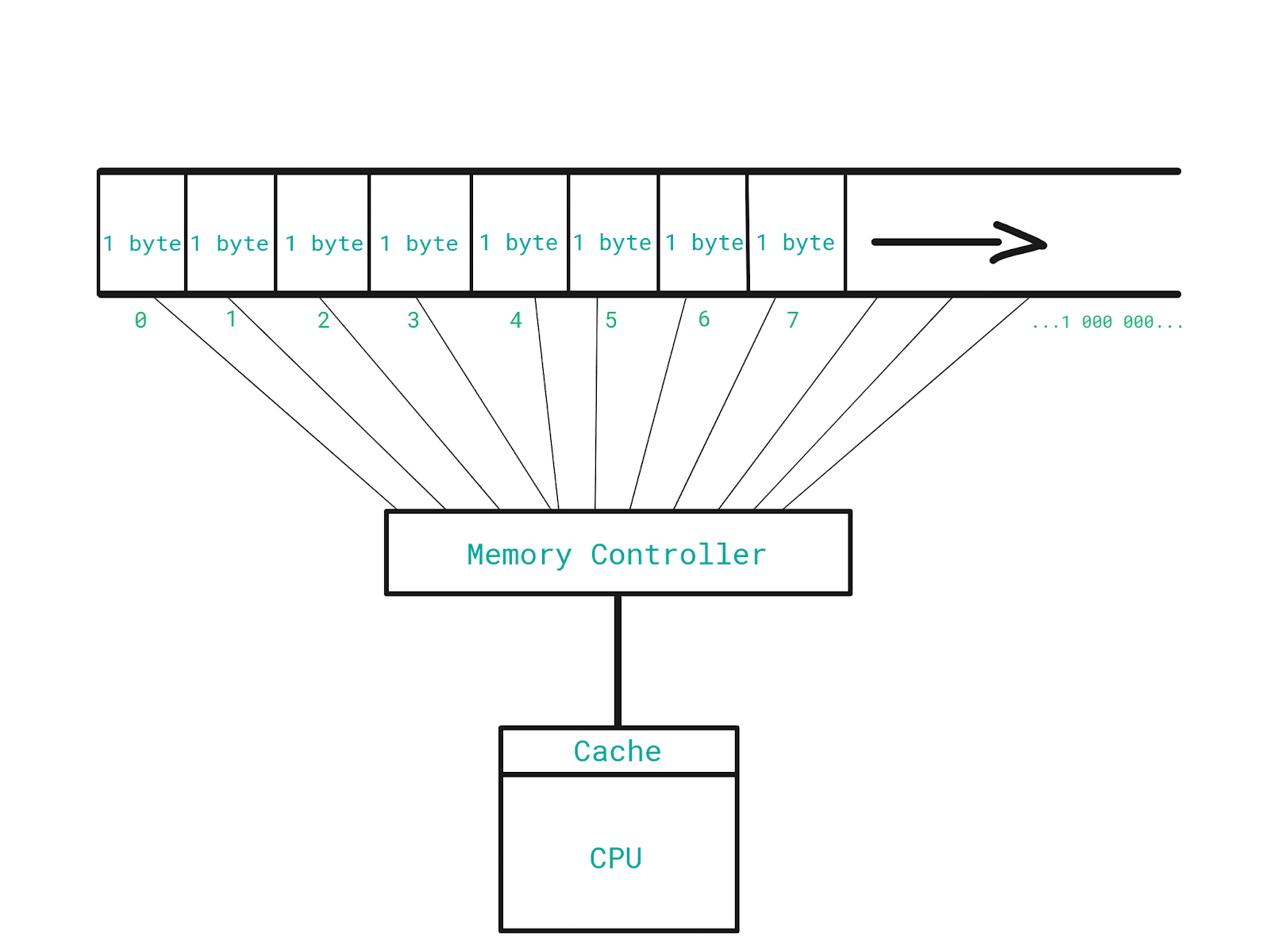
When the CPU asks for the data stored in a particular location in the memory, the memory controller also sends the data of a dozen nearby memory addresses. All of that gets stored in the cache. In other words, it gets cached.

Let’s say we want to read data stored on addresses 201, 202, 203, 204, 205 respectively.
The very first time, the data gets read from the main memory directly, and subsequent reads are going to happen from the super-fast cache.

Therefore, the CPU saves time whenever it can read something directly from the cache, because it does not have to read it from the main memory.

But, if we want to read the data stored on the addresses 200, 98 222, and then
3 591, the cache would not help here and we would have to read from the memory directly.
Why? - Because the given memory addresses are not adjacent and therefore they do not get cached.

In case you want to learn more about this, go to https://en.wikipedia.org/wiki/Locality_of_reference.

Now that we have refreshed our knowledge of how memory conceptually works, let’s get back to arrays.

Static Arrays

Arrays are fixed-length containers, containing N elements where each element is of the same size.

They are stored in contiguous/uninterrupted segments of free memory which means that all of the elements are adjacent - lined up next to each other in memory.

Just like every slot in the memory gets associated with a number, each element of an array gets associated with a number from the range [0, N-1].

This number is called an index and the process of assigning this number to each element is called indexing. (Keep in mind that indices start from 0.)

Indices reference array elements and therefore slots in memory as well.

Since we can roughly classify data structures as contiguous and linked based on whether they are built upon arrays or pointers (we will talk about them later), this tells us that arrays are building blocks of some more complex data structures.

One of the most common scenarios when programming is iterating through elements of a certain data structure. Arrays, as it turns out, are ideal for this type of problem because elements are stored next to each other in the memory. And let me remind you that reading sequential memory addresses is faster than reading the ones that are distant from each other, and now, we can see why.

Another scenario where arrays shine is accessing elements via their indices.

Let’s say that we want to have an array that stores N integers and let’s assume that each integer is 4 bytes.

The first thing we have to do is to create and initialize the array.

Basically this includes three steps:

1. Declare its type and its name
2. Create it
3. Initialise its values

int[] integerArray;	          integerArray = new int[N];     for(int i = 0; i < integerArray.length; i++) {	integerArray[i] = 0;    }

Let N be 4, that is, we want the array to store 4 integers.

Due to code elegancy, as well as the best practice, we can use a shorter form where we do all of the above in a single line.

int[] integerArray = {2, 3, 5, 8};

What happens in the memory?

Since we have 4 integers in our array, and each integer is 4 bytes, 16 bytes of contiguous free memory gets allocated.

Why 16 bytes?

We are storing 4 integers and each integer is 4 bytes - 4 * 4 = 16.

The memory is divided into slots where each slot is 1 byte, which means that 16 slots get allocated. These 16 slots are grouped into 4 blocks (4 - the size of an integer) and these blocks get indexed.

Let’s say that our computer has allocated 16 free slots starting from the address 201.

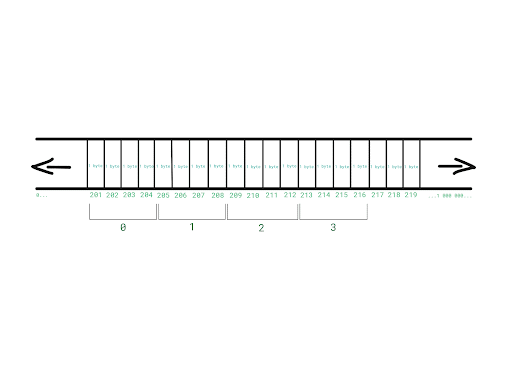
We want to access the integer with the index 3. How are we supposed to know which memory address should we go to?

Simple mathematical calculation can give us the answer. We take the starting, base address of the array and…

Hold on! How do we know which and what is this base address?

Remember how we defined our array?

int[] integerArray = {2, 3, 5, 8};

How would you read this line of code?

We could say something like this:

To the variable integerArray assign the array value…

There is a catch here.

integerArray does not somehow magically store the whole value of our array. Instead, it simply points to the array in memory. What does that mean?

This means that the value of integerArray variable is the address where the array starts in the memory - it’s base address.

And that would be enough to read the whole array.

Since we have the base address, our computer will go to that location in the memory and it is going to read byte by byte until it reaches the end of the array.

How does it know where the end is? It has everything it needs: The base address, the number of elements, and the size of each element.

Our array starts at the memory address 201, it consists of 4 integers and each integer is 4 bytes.

The end of the array is at the address 201 + 4*4 = 217.

(Try coming back to this part when we start talking about pointers).

Now we can go back to our formula.

We take the base address of the array, add the index which we want to access multiplied by the size of each element in bytes.

BaseAddress + (Index * SizeOfEachElementInBytes)
                       = MemoryAddressOfTheElement

It will be easier if we look at an example. Our array has 4 integers, of which each has a size of 4 bytes, and we wish to access the one at the index 3.

201 + (3 * 4) = 213

As computers are really good at maths, they perform these calculations unimaginably fast, in a constant time. Therefore calculating the memory address of the Nth element of an array takes constant O(1) time.

If we take into account that the memory controller has a direct connection to each slot in the memory, that means that accessing a memory address takes constant O(1) time.

In case you are unfamiliar with “O(1)” notation, it’s basically a mathematical notation that describes the following:

If we have a function or an algorithm that takes an input and processes it, what is the amount of time (or space, but let’s skip that for now) that the function/algorithm needs for execution, if the input grows larger and larger.

For now, it is enough for us to know that:

1. O(1) - means constant time complexity
2. O(n) - means linear time complexity

When we say that an algorithm is “O(1)”, or that it has constant time complexity, what we are actually saying is:

Regardless of the input size, the algorithm always needs the same amount of time for its execution.

When we say that an algorithm is “O(n)”, or that it has linear time complexity, what we are actually saying is:

As the input for this algorithm grows, the amount of time that the algorithm needs for execution grows linearly.

Let’s say that we have some algorithm that takes some data set as input and then processes it.
Let’s assume that processing of a single element lasts 1 second.

• Data set of 1 element - algorithm executes in 1 second.
• Data set of 100 elements - algorithm executes in 100 seconds.
• Data set of 1000 elements - algorithm executes in 1000 seconds.

So we have O(1) for calculating the memory address of the Nth element of an array and we have O(1) for accessing the address.

These two combined give us the most important property of arrays.

We can access array elements by their indices in constant O(1) time.

Our formula, however, works only under 2 conditions.

1. If each element of our array is of the same size
2. If our array is contiguous in memory - if elements are adjacent in terms of memory location

And this is when we introduce some limitations of arrays as data structures.

Every element must have the same size.
In case we need a big array, then we have to allocate a big chunk of contiguous free space in memory, which gets difficult when most of the space is occupied by running programs such as Slack, Visual Studio, Google Chrome...

That is the tradeoff we have to accept.

So let’s create a checkpoint here.

Arrays have extremely fast access/lookup by index - O(1), but each element has to have the same size.

For large arrays we need a big block of contiguous free space in memory.

Arrays are fixed in size - once we define the size of our array, it can not be changed during the execution of the program.

Pointer-Based Arrays

Up to this point, our array stored integers. Let’s try something else. Let’s say that we want to create an array of names.

Every name is a string - an array of characters.
Every character is essentially a number.
So, a single name would be nothing but an array of integers.
If we want to create an array of names, where a name itself is an array, then we would have to have an array of arrays.

Names, however, do not have to be the same in size (length), and one of the rules of arrays is that each element is of the same size. Well, we cannot allocate a contiguous block of memory if we do not know how long each name will be.

What we can do is to allocate, for example, 400 slots - 100 bytes for each name, just to make sure that each name fits (with the assumption that there won’t be a name longer than 100 characters). This means that all names would be adjacent in memory.

But with this approach we would need a huge chunk of contiguous free memory. This leads to inefficient memory handling which is pretty bad. Let’s try another approach.

Let’s introduce something new - a pointer.

A pointer is a variable whose value is a memory address.

How can these pointers help us now?

We could try storing each name wherever we can fit them in memory (wherever there is free space) instead of storing them one after another in our array.
Now, each element of our original array of names would simply be a pointer that points to the location in memory where the specific name is.

Because each memory address is actually an integer, our array of names would simply be an array of integers.
(Now it would be a good time to go back to the part where we explain calculating base addresses of arrays.)

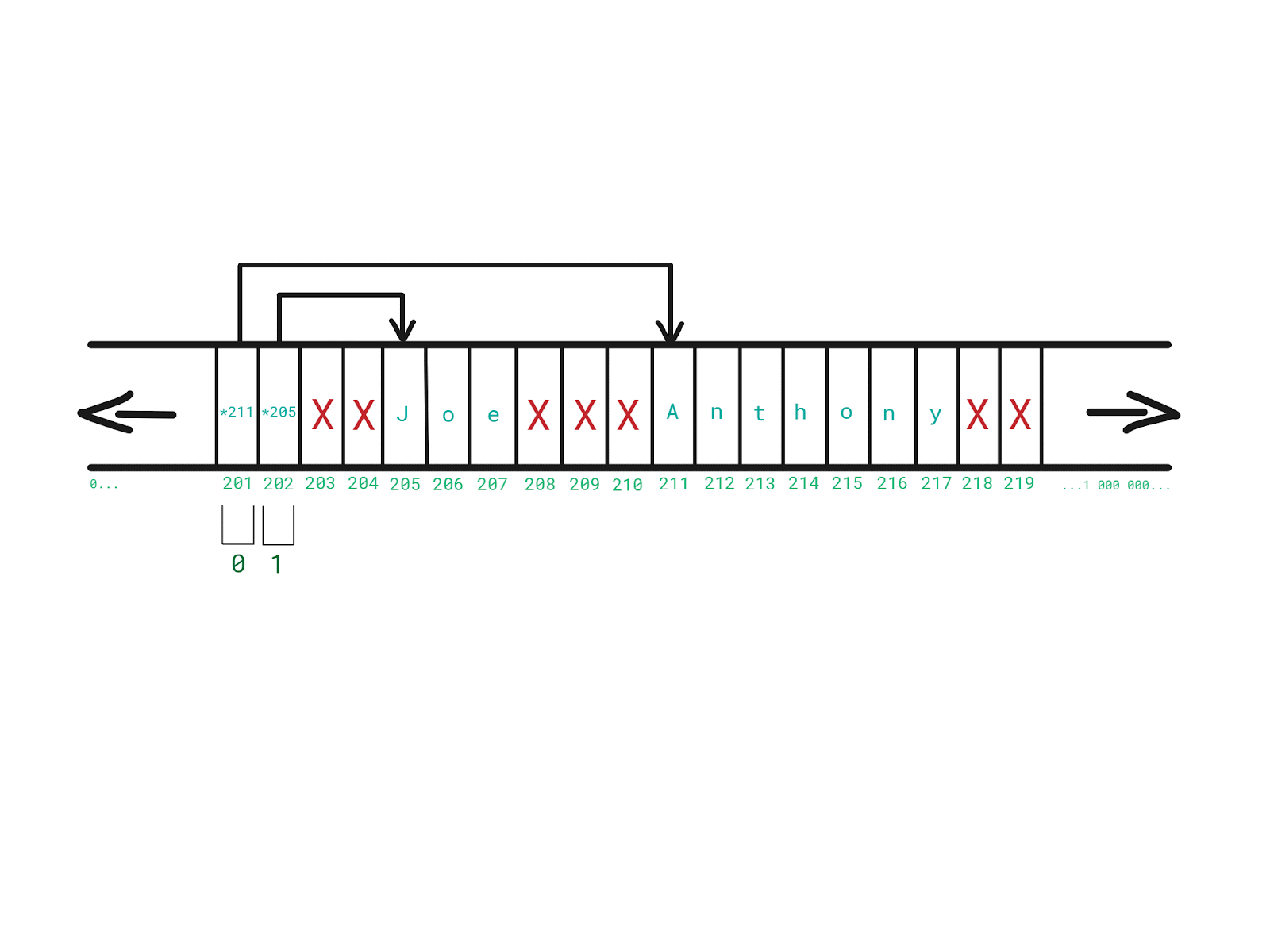
With this approach:

• Array elements can be different in size - any name can have an arbitrary length
• There is no need to allocate a big chunk of contiguous free space in memory to store each name sequentially

Unfortunately, now we introduce another tradeoff.
(You got to love software engineering right ?)

Remember when we said that reading sequential memory addresses is faster because they are subject to caching?
Our array of pointers (names) is not cache-friendly because names are now possibly scattered all over the memory.

Therefore, an array of pointers demands less contiguous free memory and can store elements that are different in size, but it is somewhat slower because it is not cache-friendly.

In algorithm analysis this “somewhat slower” is completely negligible, and we say that accessing elements by indices, even for pointer-based arrays, is still in constant O(1) time.

Dynamic Arrays

So far, we have seen that when we are declaring our array, we have to specify how many elements it will have, that is, what its size will be in advance.

Our computer has to reserve enough space in the memory for the content of our array and to make sure that nothing else uses that space. Otherwise, we would have scenarios where other programs could overwrite the content of our array.

Arrays, as we have already mentioned above, are called static arrays for the reason we outlined above.

But what if we run into a situation where we need to use an array, but, for some reason, we do not precisely know how big it will be? How can we solve this?

Well, we could create this array with some initial capacity, and program it to dynamically expand if it runs out of space for new elements - a thing called dynamic array.

A dynamic array is an array that can dynamically change its size - whether it has to shrink or expand. It is behind the scenes, most of the time implemented with a static array.

In general, the implementation consists of several things:

• Creating an internal static array with some initial capacity
• Keeping track of the elements count
• Creating a new and bigger array, copying elements from the original one, and adding the new element when there is no more space and a new element has to be added

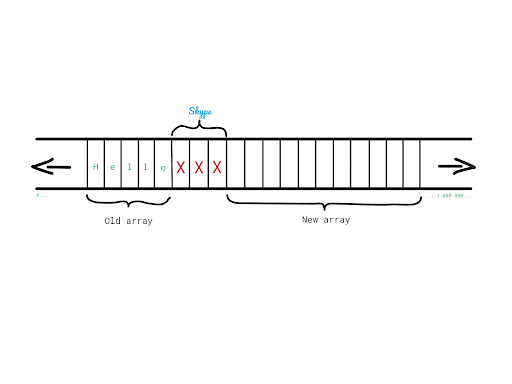
Let’s say that we have an array of characters in which we store the word Hello.

At some point, during the execution of our program, we decided that we want to append the word World to get the well-known greeting message. However, we cannot simply extend the initial array and add World next to Hello, because right after Hello we have a couple of memory slots occupied by, let’s say Skype. How can we solve this?

We could:

1. Allocate space for a new, bigger array.

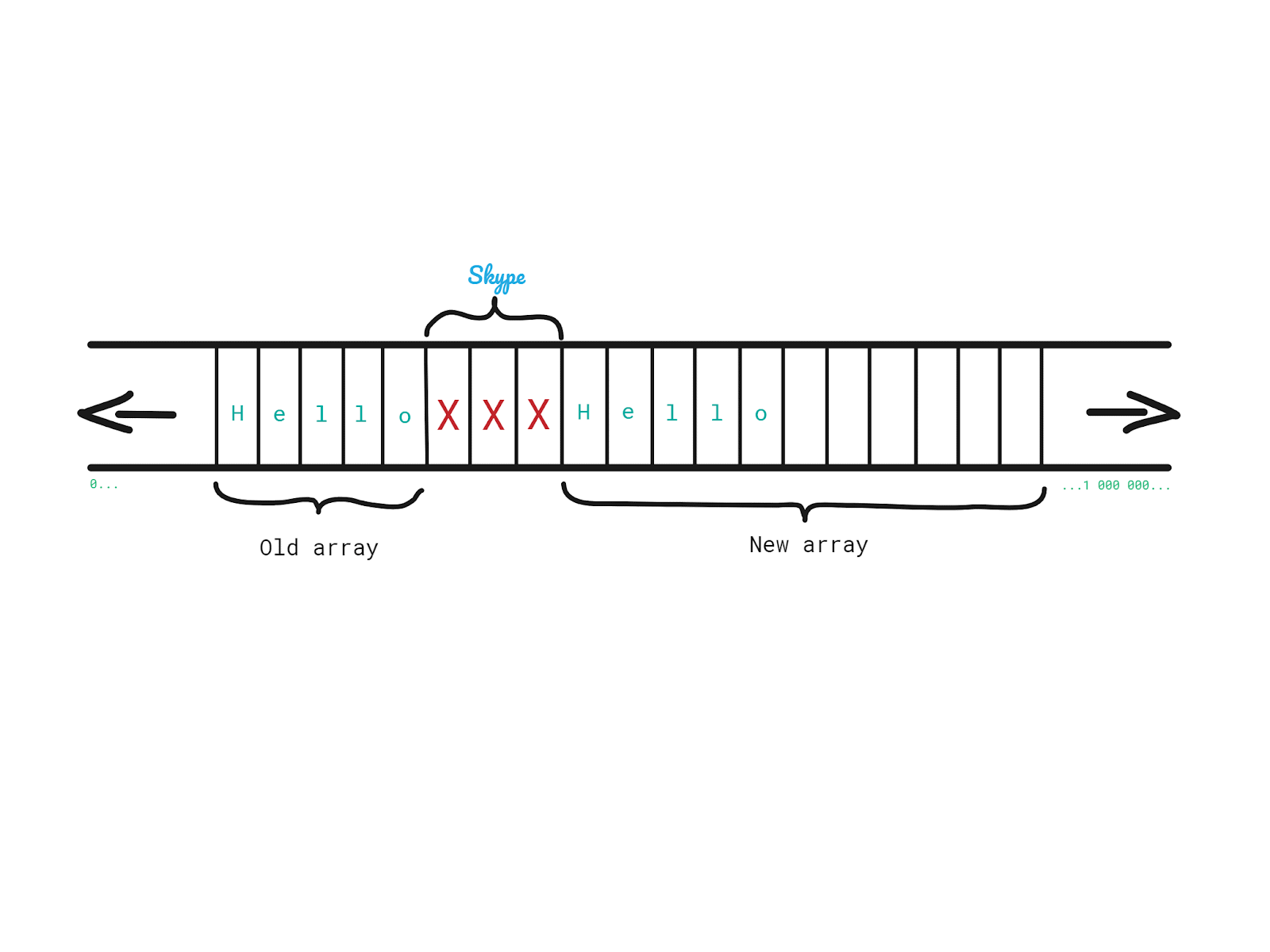
2. Copy each element from the old one into the new one.

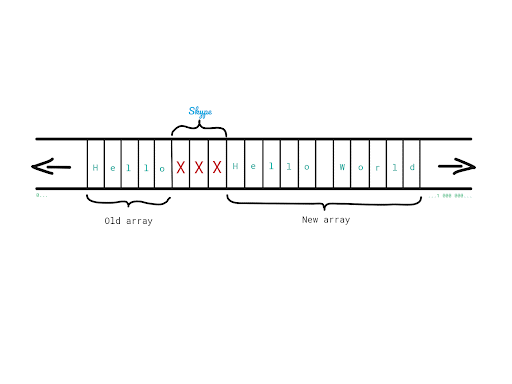
3. Add characters of “World” in the new array.

4. Free up the space occupied by the old array.

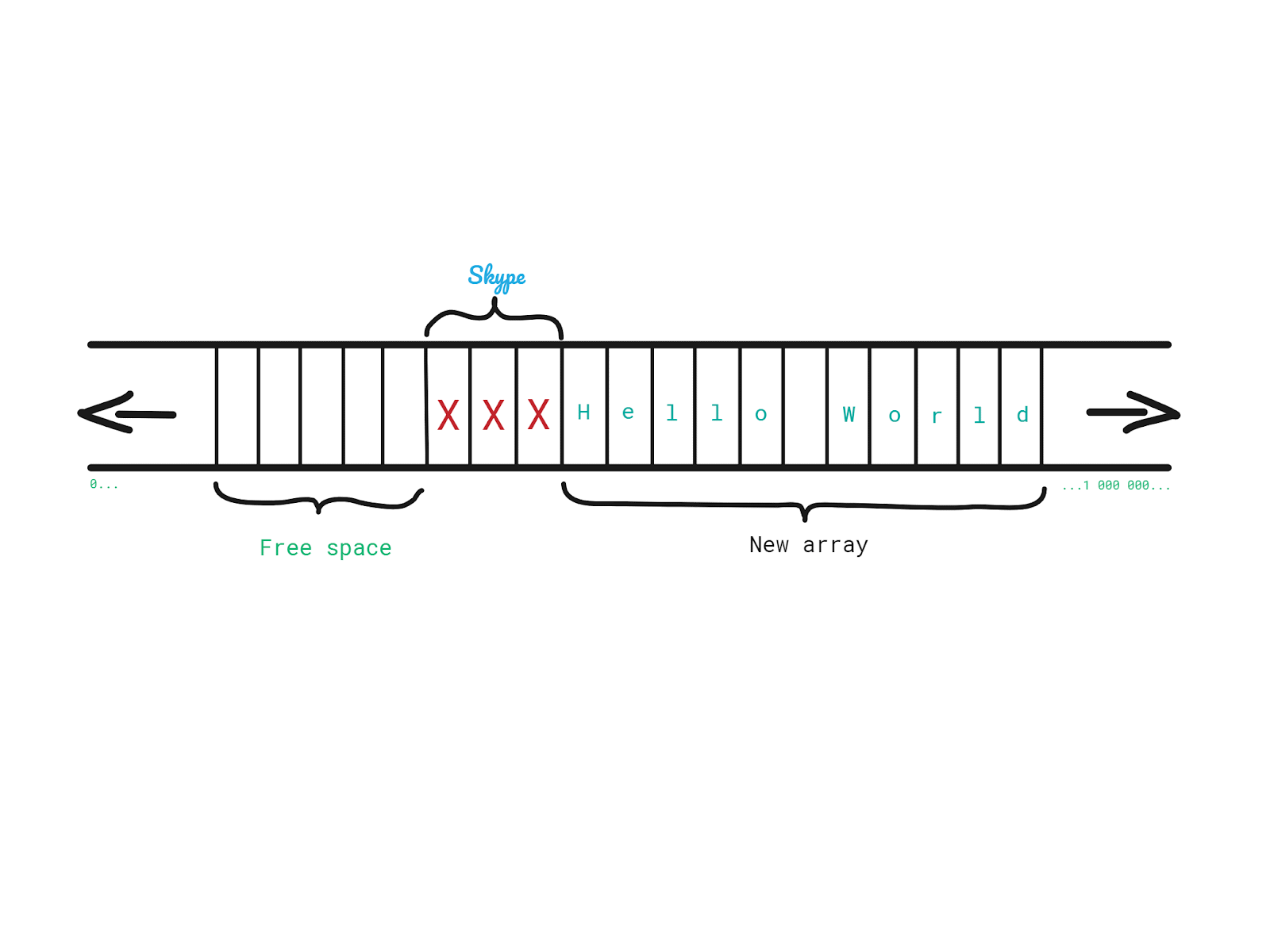
And that is a dynamic array in its essence. How long will it take to perform these steps?

If we take it for granted that allocating the new and deallocating the old array is performed in constant time, the only thing we need to decide is how long it takes to copy all the elements.

What is the worst case scenario that can happen when adding an element?

The worst scenario that can happen is that the initial array is full and that we have to allocate a bigger array and then copy all the elements into it. For this reason, appending elements into a dynamic array has a linear time complexity - O(n) - we have to copy all N elements.

So the amount of time to execute this operation increases proportionally with the growth of elements in the array. This, however, happens relatively rarely.

Only when the array goes out of space the time complexity of appending an element is O(n). In other regular cases it is O(1).

Since there are many more cases when adding is O(1) than when it is O(n), O(1) time complexity sort of negates O(n), and we say that each operation of adding an element has amortized time complexity of O(1).

In industry we mostly say that adding elements into dynamic arrays has constant O(1) time complexity.

So, dynamic arrays, compared to static ones, have the advantage of not having to specify the size in advance. However the disadvantage is that some element additions can be expensive.

Whenever we used ArrayList in Java, we used an implementation of a dynamic array.
List in C# - dynamic array, list in Python - dynamic array, and so on.

Of course, this is all abstracted away from us, and we just consume APIs of these types. But if we looked under the hood we would most certainly see some kind of dynamic array.

Key Takeways

Arrays have extremely fast - O(1) access/lookup by index.

We need enough continuous/uninterrupted free space in memory in order to store it.
All the elements have to be of the same size.

Arrays are fixed in length, and the length has to be specified upfront.

If the elements of an array are simply pointers to the actual elements, then we do not need a big chunk of contiguous, free space in memory and elements can be different in size.

The tradeoff is that this kind of array will be relatively slow because the actual elements could be scattered all over the memory so they are not subject to caching. But this tradeoff is negligible.

We use dynamic arrays when we do not want to specify the size in advance.

These too have extremely fast - O(1) access/lookup by index.

They can occasionally have expensive appends.

This is all fine, but what if we wanted to have a data structure that does not require its size to be specified in advance, nor it occasionally has expensive appends? - We will talk about linked lists in one of our next blog posts.